
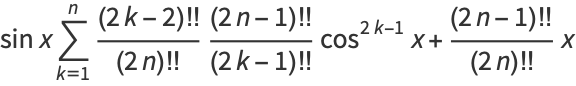
If teenagers could understand it, engineers would be able to do it even more easily. They got the idea to bring in high-school students, give them a Fortran book and access to a computer, and then see if they could learn to code relatively quickly. The boss was concerned that the time and cost needed for educating his employees in Fortran and using punch cards, not to mention buying the IBM hardware, would take them away from pressing design work. They had been doing some of this on analog computers, but felt digital was the future. At the time, the engineers wanted to convince their boss to fund new IBM computers to be used-not for business, but for engineering simulations. One of its main engineering groups worked there.
My hometown, Moline, Illinois, was the headquarters of the farm implement company John Deere. Back in the mid-60s, access to any computer for a high-school student was very unusual. This led me to think of my other obsession: computer programming. Finding even the well-known ones was challenging and error prone. It quickly became apparent that solutions were rare. These men encouraged me to follow my passion for studying such solutions. Godfrey was doing his dissertation on exact solutions. My initial fascination with such solutions led me to contact John Archibald Wheeler and his student Brendan Godfrey during an APS conference in Chicago in the late 1960s. Although this has always been difficult, Schwarzschild, Kerr, Gödel, Kaluza–Klein, Robertson–Walker, Taub–NUT and others did find now-famous solutions. Antonov, Adaptive numerical Lebesgue integration by set measure estimates, (2016), MathematicaForPrediction project at GitHub.Anyone who has tried to find exact solutions to such very complicated, coupled, nonlinear partial differential equations knows that even the straightforward, static, spherically symmetric and empty space case requires some complex tensor algebra to get to the differential equations themselves. He, Dimensionality Reducing Expansion of Multivariate Integration, 2001, Birkhauser Boston. Burrows, A new approach to numerical integration, 1. As the title says, I wonder if it is possible to calculate a Lebesgue integral in Mathematica, especially when the domain of integration is $\mathbb]


 0 kommentar(er)
0 kommentar(er)
